Unlocking Data Secrets: Your Guide To Mean, Median, Mode & Range
Table of Contents
- What are Mean, Median, Mode, and Range?
- The Mean: Your Everyday Average
- The Median: Finding the Middle Ground
- The Mode: The Most Frequent Face
- The Range: Measuring Data Spread
- Beyond Basics: Why Learn These Concepts?
- Choosing the Right Measure: Mean, Median, or Mode?
- Practical Examples and Real-World Scenarios
- FAQs: Demystifying Mean, Median, Mode, and Range
What are Mean, Median, Mode, and Range?
In the realm of statistics, when we talk about a "data set," we're referring to a collection of numbers or observations. To make sense of these collections, we often look for ways to summarize them. This is where the concepts of mean, median, mode, and range come into play. Mean, median, and mode are collectively known as "measures of central tendency." They each attempt to describe the "center" or "typical" value of a data set using a single number. The range, on the other hand, is a measure of "dispersion" or "spread," telling us how spread out the data points are. Together, these four values provide a foundational understanding of any numerical data set. They are used to define various parameters of the given data set, offering useful insights about the data studied.The Mean: Your Everyday Average
The mean, often simply called the "average," is likely the most familiar measure of central tendency. It's what you calculate when you want to find the average score on a test, the average height of a group of people, or the average salary in an organization. The mean is a powerful tool because it takes into account every single data point in the set, making it a comprehensive summary. However, this comprehensiveness can also be its weakness, especially when dealing with extreme values.How to Calculate the Mean
Calculating the mean is straightforward: you add up all the numbers in your data set and then divide by the total count of numbers you added. **Formula:** Mean = (Sum of all data points) / (Number of data points) **Example:** Let's find the mean of the following data set: 9, 4, 17, 4, 7, 8, 14. 1. **Add all data points:** 9 + 4 + 17 + 4 + 7 + 8 + 14 = 63 2. **Count the number of data points:** There are 7 data points. 3. **Divide the sum by the count:** 63 / 7 = 9 Therefore, the mean of this data set is 9. Consider another example: If a student scores 85, 92, 78, and 95 on four tests, their average (mean) score would be (85 + 92 + 78 + 95) / 4 = 350 / 4 = 87.5. This simple calculation gives us a single number that represents their typical performance across those tests.When to Use the Mean
The mean is generally the preferred measure of central tendency when your data is symmetrically distributed and does not contain extreme values, often referred to as "outliers." It provides a good summary when all data points contribute equally to the overall "average." For instance, if you're measuring the average temperature over a week, and the temperatures are relatively consistent, the mean provides a good representation. However, the mean is highly sensitive to outliers. If you have a data set like 1, 1, 4, 50, the mean would be (1+1+4+50)/4 = 56/4 = 14. Here, the single extreme value of 50 significantly pulls the mean upwards, making 14 not very representative of the typical values (1, 1, 4). In such cases, using the mean can be misleading, and other measures might be more appropriate. This is crucial in fields like economics, where a few extremely high incomes can skew the "average salary" to appear higher than what most people actually earn.The Median: Finding the Middle Ground
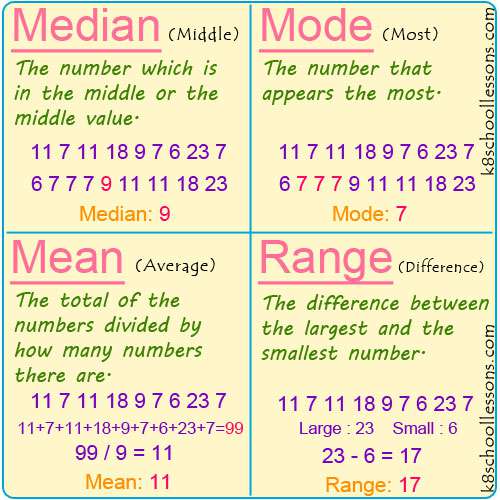
The median is the middle value in a data set when the data points are arranged in numerical order. Unlike the mean, the median is not affected by extremely high or low values, making it a more robust measure of central tendency in the presence of outliers. It truly represents the "middle" point of your data.Calculating the Median
To find the median, the first crucial step is always to arrange your data set in ascending (or descending) order. **Steps:** 1. **Order the data:** Arrange all data points from smallest to largest. 2. **Find the middle value:** * **If the number of data points is odd:** The median is the single middle number. * **If the number of data points is even:** The median is the average of the two middle numbers (add them together and divide by 2). **Example (Odd number of data points):** Let's use the same data set: 9, 4, 17, 4, 7, 8, 14. 1. **Order the data:** 4, 4, 7, 8, 9, 14, 17 2. **Find the middle value:** There are 7 data points. The middle value is the 4th one (since (7+1)/2 = 4). 4, 4, 7, **8**, 9, 14, 17 The median is 8. **Example (Even number of data points):** Consider the data set: 10, 15, 20, 25, 30, 35. 1. **Order the data:** (Already ordered) 10, 15, 20, 25, 30, 35 2. **Find the middle value:** There are 6 data points. The two middle values are the 3rd and 4th ones. 10, 15, **20**, **25**, 30, 35 The median is the average of 20 and 25: (20 + 25) / 2 = 45 / 2 = 22.5.Why the Median Matters
The median is particularly useful when dealing with skewed data or data sets that contain outliers. For instance, when discussing household income, the median income is often a more accurate representation of what a "typical" household earns than the mean income, precisely because a few extremely wealthy individuals can significantly inflate the mean. The median gives a truer picture of the central tendency without being distorted by these extreme values. It's often used in real estate (median home prices) and socio-economic studies.The Mode: The Most Frequent Face
The mode is the simplest of the measures of central tendency to understand: it is the number that appears most frequently in a data set. Unlike the mean and median, the mode can be used for non-numerical (categorical) data as well as numerical data.Identifying the Mode
To find the mode, you simply count the occurrences of each number in your data set. **Steps:** 1. **Count occurrences:** Tally how many times each unique number appears. 2. **Identify the most frequent:** The number (or numbers) that appear most often is the mode. **Example:** Let's use our data set again: 9, 4, 17, 4, 7, 8, 14. 1. **Count occurrences:** * 4 appears 2 times * 7 appears 1 time * 8 appears 1 time * 9 appears 1 time * 14 appears 1 time * 17 appears 1 time 2. **Identify the most frequent:** The number 4 appears most frequently (2 times). The mode of this data set is 4. **Important Notes on Mode:** * **No Mode:** A data set may have no mode if all numbers appear with the same frequency (e.g., 1, 2, 3, 4, 5). * **Multiple Modes (Bimodal, Multimodal):** A data set can have more than one mode if two or more numbers share the highest frequency (e.g., in 1, 2, 2, 3, 3, 4, both 2 and 3 are modes).Practical Applications of the Mode
The mode is particularly useful for identifying the most popular or common item in a set. For example, if a shoe store wants to know which shoe size they should stock the most, they would look at the mode of shoe sizes sold. If a car manufacturer wants to know the most popular color for a particular model, they would find the mode of color choices. It's also invaluable in surveys to determine the most common opinion or preference. While the mean and median require numerical data, the mode can be applied to qualitative data, such as favorite colors, types of cars, or yes/no responses, making it uniquely versatile.The Range: Measuring Data Spread
While mean, median, and mode tell us about the center of a data set, the range tells us about its spread or dispersion. It's the simplest measure of variability, indicating the total span of the data.Calculating the Range
The range is found by subtracting the smallest value in the data set from the largest value. **Formula:** Range = (Largest value) - (Smallest value) **Example:** Using our familiar data set: 9, 4, 17, 4, 7, 8, 14. 1. **Identify the largest value:** 17 2. **Identify the smallest value:** 4 3. **Subtract the smallest from the largest:** 17 - 4 = 13 The range of this data set is 13.Limitations and Insights from Range
The range provides a quick and easy way to understand the spread of data. A small range indicates that the data points are clustered closely together, while a large range suggests that they are widely dispersed. However, like the mean, the range is highly susceptible to outliers. A single extremely high or low value can drastically inflate the range, making it less representative of the typical spread of most data points. For example, if a class scores between 70 and 90 on a test, but one student scores 10, the range would be 90 - 10 = 80, which doesn't reflect the typical spread of 20 points for the majority of the class. Despite this limitation, the range is a useful preliminary measure for understanding the overall variability within a data set.Beyond Basics: Why Learn These Concepts?
Learning about mean, median, mode, and range goes far beyond just solving math problems in a classroom. These concepts are fundamental building blocks for understanding statistics and data analysis, skills that are increasingly vital in everyday life and almost every professional field. From interpreting news reports about economic trends to making personal financial decisions, the ability to make sense of numbers and data is invaluable. These statistical measures help you summarize large groups of data efficiently. Imagine trying to understand the performance of a large company by looking at every single employee's salary. It would be overwhelming. Instead, knowing the average (mean) salary, the typical (median) salary, or the most common (mode) salary provides quick, actionable insights. Similarly, understanding the range of salaries tells you about the disparity within the company. These concepts form the basis for more advanced statistical analysis, helping professionals in fields like finance, healthcare, marketing, and science to draw robust conclusions, identify significant patterns, and predict future outcomes. They empower you to critically evaluate information, whether it's a study on public health, a report on consumer behavior, or a personal budget. In essence, they provide the lens through which we can transform raw numbers into meaningful stories and actionable intelligence.Choosing the Right Measure: Mean, Median, or Mode?
While the mean, median, and mode are all valid measures of central tendency, their appropriateness varies depending on the nature of your data and the specific question you're trying to answer. Knowing when to use which average is a key aspect of effective data analysis. 1. **When to Use the Mean:** * **Data Distribution:** Best for data that is symmetrically distributed without significant outliers. * **Data Type:** Numerical data. * **Purpose:** When you want to include every data point's value in the calculation and are interested in the true "balancing point" of the data. * **Example:** Average test scores in a class where scores are generally well-distributed, or average height of a population. 2. **When to Use the Median:** * **Data Distribution:** Ideal for skewed data or data sets with extreme values (outliers). * **Data Type:** Numerical data. * **Purpose:** When you need a measure that is not influenced by unusually high or low values, providing a more representative "typical" value. * **Example:** Median household income, median home prices, or average age of a class if there are a few very old or very young individuals. 3. **When to Use the Mode:** * **Data Distribution:** Useful for any type of data, including categorical data. * **Data Type:** Numerical or non-numerical (qualitative) data. * **Purpose:** When you want to identify the most frequent or popular item, category, or value. * **Example:** Most common shoe size sold, most preferred brand of soda, or the most frequent number of siblings in a survey. For instance, if you're looking at the number of medals the U.S. has won over the last six Summer Olympics, and one year had an exceptionally low or high number due to unusual circumstances, the median might give a more stable representation of typical performance than the mean. If you're studying customer preferences for a product, the mode will tell you which feature is most popular, which neither the mean nor median can do for qualitative data. Understanding these nuances allows you to choose the most appropriate statistical measure to accurately describe your data and avoid misleading interpretations.Practical Examples and Real-World Scenarios
The concepts of mean, median, mode, and range are not confined to textbooks; they are integral to understanding various real-world situations. Let's explore a few more practical applications: **1. Sports Statistics: Olympic Medals** Imagine we're analyzing the number of medals the U.S. has won over the last six Summer Olympics: 110, 104, 121, 104, 112, 104. * **Mean:** (110 + 104 + 121 + 104 + 112 + 104) / 6 = 655 / 6 ≈ 109.17 medals. This is the average number of medals won. * **Median:** First, order the data: 104, 104, 104, 110, 112, 121. Since there are 6 data points (even), the median is the average of the two middle numbers (104 and 110): (104 + 110) / 2 = 214 / 2 = 107 medals. * **Mode:** The number 104 appears three times, which is more than any other number. So, the mode is 104 medals. * **Range:** Largest (121) - Smallest (104) = 17 medals. This tells us the spread between the highest and lowest medal counts. From this, we can see that while the average is around 109, the most frequent medal count was 104, and the typical performance (median) was 107. The range of 17 shows there isn't a massive fluctuation in performance over these Olympics. **2. Business and Economics: Employee Salaries** Consider a small company with employee salaries (in thousands of dollars): 30, 35, 40, 45, 50, 60, 200. * **Mean:** (30+35+40+45+50+60+200) / 7 = 460 / 7 ≈ 65.71 thousand dollars. * **Median:** Ordered: 30, 35, 40, **45**, 50, 60, 200. The median is 45 thousand dollars. * **Mode:** There is no mode, as all numbers appear only once. * **Range:** 200 - 30 = 170 thousand dollars. In this scenario, the mean salary (approximately $65,710) is significantly higher than what most employees earn, due to the outlier salary of $200,000 (likely a CEO or high-level executive). The median salary ($45,000) provides a much more realistic picture of what a "typical" employee earns in this company. The large range ($170,000) highlights the significant income disparity. This example clearly illustrates why the median is often preferred for income data. **3. Education: Test Scores** A class of 10 students had the following scores on a math quiz: 75, 80, 85, 70, 90, 80, 95, 65, 80, 75. * **Mean:** (75+80+85+70+90+80+95+65+80+75) / 10 = 795 / 10 = 79.5. The average score. * **Median:** Ordered: 65, 70, 75, 75, **80**, **80**, 80, 85, 90, 95. The two middle numbers are 80 and 80. (80+80)/2 = 80. The median score. * **Mode:** The score 80 appears three times, which is more than any other score. The mode is 80. * **Range:** 95 - 65 = 30. The difference between the highest and lowest score. Here, the mean, median, and mode are quite close (79.5, 80, 80), suggesting a relatively symmetrical distribution of scores without extreme outliers. This indicates that the class performance is quite consistent around the 80 mark. These examples demonstrate how mean, median, mode, and range provide distinct yet complementary insights into data, enabling a more nuanced and accurate understanding of the information at hand.FAQs: Demystifying Mean, Median, Mode, and Range
We've put together some frequently asked questions about mean, mode, median, and range to help you understand these concepts even better. **1. Why do students learn about mean, mode, median & range?** Learning about mean, mode, median, and range helps students develop crucial analytical skills. These concepts are foundational for making sense of numbers and data in everyday life, from understanding news statistics to managing personal finances. They teach students how to summarize information, identify patterns, and draw conclusions from raw data, which are essential skills for problem-solving and critical thinking in any field. It's about empowering individuals to interpret the world around them, which is increasingly driven by data. **2. What is the difference between mean, median, and mode?** The mean is the average (sum of all values divided by the count of values). The median is the middle value when the data is ordered. The mode is the most frequently occurring value. They are all measures of central tendency, but they define "center" differently. The mean is sensitive to outliers, the median is robust to outliers, and the mode identifies the most common value, even for non-numerical data. **3. When should I use the mode, median, or mean?** * **Mean:** Use when data is symmetrical and free of extreme outliers. It's good for calculating true averages. * **Median:** Use when data is skewed or contains outliers, as it provides a more representative "typical" value that isn't distorted by extremes. * **Mode:** Use when you need to find the most frequent item or category, especially useful for categorical (non-numerical) data. **4. Can a data set have more than one mode?** Yes, a data set can have multiple modes. If two or more numbers share the highest frequency, then all of them are considered modes. For example, in the data set {1, 2, 2, 3, 3, 4}, both 2 and 3 are modes. If all numbers appear with the same frequency, the data set has no mode. **5. Is the range a measure of central tendency?** No, the range is not a measure of central tendency. Mean, median, and mode are measures of central tendency, describing the "center" of the data. The range is a measure of dispersion or spread, indicating how spread out the data points are from the lowest to the highest value. **6. Where can I find more resources to practice these concepts?** Many educational platforms offer resources. For instance, BBC Bitesize Key Stage 3 Maths provides excellent explanations and practice. You can also find free PDF worksheets, video lessons, and interactive games online that help you learn how to calculate and interpret the mean, median, mode, and range with examples. Many descriptive statistics calculators are also available online that will generate step-by-step explanations on how to find these values for a given data set. **7. Are these concepts used in real-world statistical analysis?** Absolutely. These are fundamental to descriptive statistics and are used in countless real-world situations. From analyzing average salaries in organizations and understanding the median age of a population to determining the most popular product features or assessing the variability in stock prices, mean, median, mode, and range provide essential insights for researchers, businesses, governments, and individuals alike. They are the initial steps in understanding any large group of collected data.Conclusion
The mean, median, mode, and range are more than just mathematical calculations; they are indispensable tools for interpreting and understanding data in our daily lives. By mastering these four concepts, you gain the ability to quickly summarize numerical information, identify typical values, understand data spread, and make more informed decisions. Remember that each measure serves a unique purpose, and the "best" one to use depends entirely on the nature of your data and the insights you seek. We hope this comprehensive guide has demystified these essential statistical concepts for you. Now, armed with this knowledge, you are better equipped to navigate the sea of data that surrounds us. What data set will you analyze first? Share your thoughts or any questions you might have in the comments below, or explore other insightful articles on our site to deepen your understanding of data and its power!
Mean, Median, Mode and Range Posters | Teaching Resources

Mean, Median, Mode, and Range. | Math resources, Studying math, Math
Median Mode Mean and Range | How to find median Mode Mean Range